三维重建方法

Posted on | Views:

小孔相机模型

https://blog.csdn.net/lsh_2013/article/details/47615309

坐标系及其转换

相机模型中有四个重要的坐标系

  • 1.世界坐标系 ($X_w, Y_w, Z_w$)，世界坐标系就是物体在真实世界中的坐标
  • 2.像平面坐标系($x, y$)，注意这个是像平面的物理坐标，单位是实际物理长度，如1cm等
  • 3.像素坐标系($u, v$)，注意这个是像平面的像素坐标，是按个算的像素位置，如(3, 5)是指第三行第五个像素。
  • 4.相机坐标系($X_c, Y_c, Z_c$), 是以相机为中心，相机朝向为坐标轴方向的坐标系，实际上就是世界坐标系进行了一定的线性变换得到的新的坐标系。(显然从世界坐标系转换到相机坐标系物体都是保持线性关系的，不会发生扭曲，相对位移等，因此这就是个仿射变换)

相机坐标系和世界坐标系的变换

既然知道了这就是个仿射变换，那么其实转换形式也就定下来了。实际上就是一个三维旋转平移矩阵. 点击这里复习三维坐标系旋转平移的各种表示方法： https://zhuanlan.zhihu.com/p/45404840
三维的旋转矩阵就是一个3x3的矩阵，是由三个旋转矩阵按照欧拉角的顺规顺序点乘得来的，维基百科有所有12种顺规的旋转矩阵表示：https://en.wikipedia.org/wiki/Euler_angles
显然，旋转矩阵，加上平移分量，就可以用齐次坐标表示相机坐标系和世界坐标系的转换了。
反正得到的旋转矩阵是这样的形式：

像素坐标系与像平面坐标系转换

20150813170616321
可以看到，像素坐标系和像平面坐标系还是比较容易转换的，其中一个关键参数就是一个像素的物理大小是多少，假设一个像素的物理大小是$(dx, dy)$，那么单位面积的像素个数就是$(\frac{1}{dx}, \frac{1}{dy})$转换关系就是：

相机坐标系与像平面坐标系关系

也就是成像关系，符合相似三角形性质

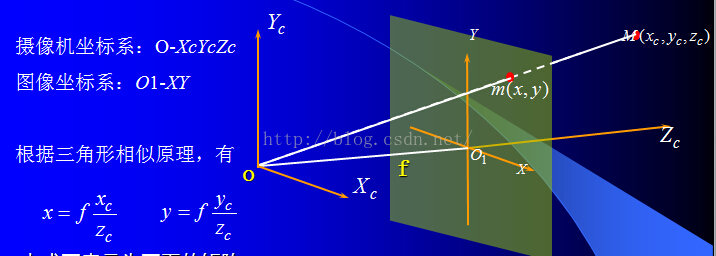
20160126094724700
我们可以看到

综合上述三个转换关系，我们能够得到从世界坐标到像素坐标的转换关系

其中：

所以

注意，我们看到，这些矩阵计算过程中，是需要保留中间结果$Z_C$的，不能直接混在一起乘过去。实际上，K是OpenGL根据glViewPort计算出来的，用来决定OpenGL的像平面（三维空间里的二维平面， 范围是x, y都是[-1, 1]）和实际渲染的像素（实际渲染结果）的比例，因此在GLSL里面我们完全可以将所有矩阵都乘完，此时所有的矩阵等效于一个$M$，此后我们就管不着了，到了OpenGL内部去了，此时OpenGL会自动除以第三个参数，也就是$Z_C$，将[-1, 1]范围内的留下，然后再乘以K。比如一个常见的片段着色器可以这么写：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
layout (location = 2) in vec2 aTexCoord;

out vec2 TexCoord;

uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
	gl_Position = projection * view * model * vec4(aPos, 1.0);
	TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}

实际上，到gl_Position为止，依然还是相机坐标，还没渲染到像平面（即还没除以$Z_C$），也显然没到像素(即还没乘以K)。而OpenGL的相机内参K非常简单，那就是：一般而言，f/dx = 渲染宽度，可以取img.cols/2, f/dy是渲染高度，可以取img.rows/2 ，也就是，像平面坐标(1, 1)映射到图像像素那就是(x=cols/2, y=rows/2)，以图像中心为坐标原点，刚好是右上角，所以不要觉得神奇，就是个约定。

OpenGL这个相机是假的，所以K是已知的，但是实际的相机K可不是这么简单的。K的参数完全由相机决定，称之为内部参数矩阵，而M的参数则由相机的位置所决定，称之为外部参数矩阵。实际成像模型，考虑到相机镜头加工不完善，还会存在畸变，比如由于多个光学镜头的主光轴不完全共线产生的径向和切向畸变。参考：https://blog.csdn.net/dcrmg/article/details/52950141
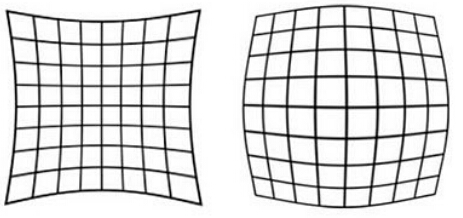
切向畸变是由于透镜本身与相机传感器平面（成像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。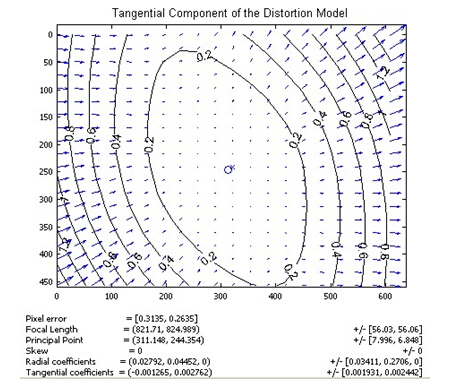
切向畸变

径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲，这种畸变在普通廉价的镜头中表现更加明显，径向畸变主要包括桶形畸变和枕形畸变两种。以下分别是枕形和桶形畸变示意图：
径向畸变

0%